Death-by-Expert – a Cross-country Study

A few weeks ago a federal judge ruled that the CDC had no business imposing a “mask mandate” on travelers.  Precious the mandate was, however, to Anthony Fauci.  But, having lost his precious, he could not help himself.  He could not help but emerge from his cave and declare that non-expert judges have no business countermanding self-anointed experts.  He made the rounds on the television news.  “This is a public health matter, not a judicial matter,” he declared on CBS News.[1]  “[T]he  principle of a court overruling a public health judgment by a qualified organization like the CDC is disturbing in the precedent it might send.”  He declared much the same over on FOX news: “[T]his is a public health decision, and I think it's a bad precedent when decisions about public health issues are made by people, be they judges or what have you, that don't have experience or expertise in public health.”[2]

Fauci’s understanding of the role of “experts” in government is hardly a new one.  Plato, for example, made his case for government-by-expert in Republic.  Taoist sages made a point of ridiculing the same thing.  They had more respect for complex processes—processes that might defy the efforts of the experts to control them.  Meanwhile, one can find enthusiastic expressions of government-by-expert in such tomes as Woodrow Wilson’s The State (1889), Vladimir Lenin’s The State and Revolution (1917), and James Landis’s The Administrative Process (1938).  Fauci could just as well have emerged from the pages of The Administrative Process: Government-by-expert should be insulated from political oversight (democratic process and free elections) and from judicial review; courts have no business restraining the rule of the expert class. Landis is explicit about that.

Meanwhile, our own self-anointed health experts have this irritating way of ignoring inconvenient facts.  The facts would include the results of Denmark’s DANMASK-19 “random control trial.”  That experiment did not yield a statistically distinguishable difference (as measured by coronavirus infections) between masking up and going mask free, although that did not discourage one of the study’s authors from advocating for masking up.  (I recommend this interview by Freddie Sayers, an excellent interviewer, with that same author: https://unherd.com/thepost/danish-mask-study-professor-protective-effect-may-be-small-but-masks-are-worthwhile/.)  It gets worse in that the DANMASK-19 study did not take up the question of potential negative effects of mask-wearing.

This short note takes up three other dimensions of expert guidance.   (1) The experts asserted that the mRNA therapies—the ersatz “vaccines”—would preclude infection and death.  Indeed, the Journal of the American Medical Association went so far as to claim that, by having availed ourselves of the “vaccines,” “millions of COVID-19 cases and hospitalizations have been prevented and hundreds of thousands of lives saved”.[3]  (2) The experts also asserted that “non-pharmacological interventions” (NPI’s) such as lockdowns would save lives and prevent infection.  (3) The experts really were chasing their tails in that they tended to increase the severity of NPI’s in the months after fatalities had been increasing, … but at the same time that case counts would be decreasing.  The experts were always reacting to events, but there is no evidence that their interventions actually reduced cases or fatalities.

In this note I examine the performance of NPI’s and mRNA therapies across countries.  I deploy data generously compiled for us by Our World in Data at https://ourworldindata.org/coronavirus.  Our World in Data aggregates and updates publicly available data and has become an important source for independent researchers and reporters.

I discuss results relating to three sets of statistical exercises.  First, I examine the lag (if any) month to month in the implementation of NPI’s.  One will be able to see that the authorities tended to ramp up NPI’s as monthly rates of coronavirus cases mounted, but, just as they were ramping up, rates of new cases tended to decline. 

Second, I examine the wide variation in fatalities attributed to coronavirus infections, and I examine this variation in conjunction with variation in NPI’s and vaccine uptake across countries.  Third and finally, I do the same type of exercise, except I apply it to variation in coronavirus cases.

According to the experts, more aggressive NPI regimes and more aggressive vaccine uptake should have induced lower COVID mortality, fewer COVID cases, and, ultimately, lower all-cause mortality.  It turns out, however, that the data tell a different story.  It is hard not to conclude that NPI’s and vaccines induced higher caseloads, higher total mortality and even higher mortality attributed to COVID.  Many of the experts may have known that they were talking nonsense, but all of the experts who signed on to NPI’s and the ersatz “vaccines” proved to be way off base.

I now ask for the reader’s indulgence in that I have to take the reader through some discussion of regression analysis and the estimation of “elasticities”.  I give this some attention, because I hope to situate the reader to gauge the quality of the evidence.  (If you don’t have time for that, just skip ahead to the tables, but make sure you understand “elasticities.”)  The data are good, not perfect.  They are mostly imperfect insofar as they do not span all countries.  Data from some countries are more complete than others.  In certain analyses, for example, African countries virtually disappear, and yet it was just such countries that experienced very little COVID-induced mortality and less in the way of vigorous vaccination programs.  The lower age distribution would have very much to do with that.  COVID, as we know, inflicted its toll on the very elderly and the infirm, not on younger, healthy people.

The data do allow us to craft defensible answers to certain questions, but they are not good enough to apply regression analysis to the question that motivated me to craft this essay: Did NPI’s and vaccination campaigns induce any statistically discernible effects (positive or negative) on total, all-cause mortality?  We can say some things about all-cause mortality or (the same thing, really), “excess mortality,” but the cross-country data I examine here don’t obviously support regression analysis.  I will explain further below.

For most analyses I run regressions of the log-linear form lny = α + β lnx + ε where y indicates a measure of performance (such as total COVID fatalities over 2020-2021), and x indicates a factor that likely informs performance (such as a measure of the age distribution of a country’s population.)  The α term is a constant and the β is the performance coefficient of interest.  The ε indicates a random error.  The reader may recognize β as an “elasticity” in that differentiating y with respect to x and rearranging yields β = (Δy/y)/( Δx/x).  What this little formula means is that tweaking the x by Δx  (“delta x”) yields a percentage change in x equal to Δx/x.  That tweak induces a percentage change in y of Δy/y.  Thus, β equals the ratio of the percentage change in y over the percentage change in x.  Stated differently, a 1% change in x will induce a β% change in y.  A 2% change in x will induce a 2β% change in y.

In place of a “log-linear” regression of the form lny  = α + βlnx + ε, one could just have well posed a linear equation y  = α + βx + ε.  We would have to assign a somewhat different interpretation to the estimate of the β coefficient, but it turns out that logarithmic forms often do a better job fitting data that are strictly non-negative, and a lot of quantities we will examine, like median age by country, are strictly non-negative.  It is just the way of the universe.

Regression analysis of coronavirus caseloads –

To warm things up, let’s start with an analysis of coronavirus caseloads.  For starts, I regress the (natural log of) total cases accumulated over 2020-2021 on (the natural log of) total vaccinations over 2020-201 and (the natural log of) a measure of the average “stringency” of NPI’s adopted in a given country over 2020-2021.  I use the “Government Response Stringency Index” reported by OWID at https://github.com/owid/covid-19-data/tree/master/public/data.  The index is a “composite measure based on 9 response indicators including school closures, workplace closures, and travel bans, rescaled to a value from 0 to 100 (100 = strictest response)”.  I thus end up with a regression equation that looks like:

ln(Cases) = α + β ln(Vaccinations) + γ ln(Stringency) + ε

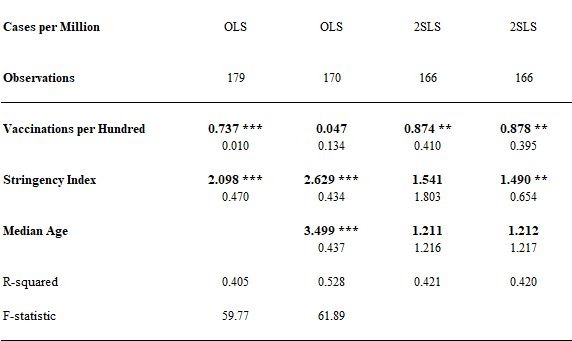
In this equation we have two elasticities to estimate, one on total vaccinations (β) and the other on stringency (γ).  Not all 228 countries in the data set provide data sufficient to include them in the analysis.  This particular regression works out of a subset of 179 countries. 

An hypothesis implicit in this regression analysis is that vaccinations and stringency may affect total case loads, but there is no feedback from total caseloads into total vaccinations and the stringency of a country’s NPI regime.  The implicit hypothesis, of course, may not be true.  One can imagine that, if and when cases increased, the authorities in a given country may have increased the stringency of its NPI regime.  The authorities may have bought into the conceit that they have to appear to “Do Something!”  Imposing harsh lockdowns and mask mandates would give them the appearance of doing something.  One could also imagine that evidence of increasing cases may have induced some panic in the population; the authorities may have made a point of aggravating that panic; demand for vaccinations may have increased.

For now, let’s ignore the prospect of feedback and just accept this naïve regression equation as is.  The experts and the establishment media said nothing about feedback.  They seemed to suggest that there would be no feedback, just get your vaccinations and “Stay home – Save Lives!”  This equation models the expert guidance as is.  And what does estimation of the two elasticities β and γ yield in this model?  Estimation by ordinary least squares (OLS) yields:

(1) A 1% increase in vaccinations would induce on average, a 0.737% increase in cases.  (That is, β = 0.737.)  The estimate of the standard error of the coefficient estimate is 0.010; the coefficient estimate is statistically significant.

(2) A 1% increase in the stringency of the NPI regime would yield, on average, a 2.098% increase in cases.  That estimate is also statistically significant.

The estimated equation yielded an R-squared in excess of 40%.  Not bad.

I reproduce all of these results in the first column of the following table.  The other three columns in the table feature results that I will discuss further on:

The numbers in bold indicate coefficient estimates.  The numbers below them indicate standard errors.  Smaller standard errors indicate greater degrees of statistical significance.  The indications ***, ** and * identify levels of statistical significance in excess of the 1%, 5% and 10% levels, respectively.

Note what all this means.  Vaccinations and NPI’s have the appearance of sharply increasing caseloads.  If the experts were right—if vaccinations and NPI’s would decrease caseloads and there is no feedback—then we would hope to see some evidence of that in a naïve regression equation. We do not.

I say that everything “has the appearance” of being this or that, because the results depend on us having posed a model that at least approaches the right model of how the world works.  Now, no equation will ever be entirely correct, but we can hope that we at least capture the most important action with a given equation, and we can hope that a simple equation, not too larded up with variables and elaborate structure, can do the job.  A danger of posing larded up, over-engineered regression models is that the analyst may confuse the real action with noise.  Indeed, beware over-engineered or heavily larded regression analyses.  Has the analyst appealed to over-engineered analysis in order to bury unpalatable results and to torture the data into telling factually incorrect but politically palatable results?  If we can’t see the basic proposition in a relatively simple regression model, then we need a good to reason to argue why a more elaborate model will do the job.

One can imagine that a larded up or over-engineered analysis could have the appearance of overturning the conclusion that NPI’s and vaccinations induce higher caseloads, but let us contemplate two possibilities: First, confounding factors not included in the naïve regression equation might yet be driving the most important action.  Second, there may be important feedback between caseloads, vaccination and stringency.

Consider the first possibility.  What happens when we include some measure of the age distribution in a more elaborate equation?  That is, what happens when pose an equation like:

ln(Cases) = α + β ln(Vaccinations) + γ ln(Stringency) + δ ln(Median Age) + ε

I present the results from estimating coefficients from this equation in the second column of the table above.  What do we see?  The effect of vaccinations on caseloads disappears and appears to be basically zero.  Median Age seems to explain much of the action.  A 1% increase in the median age translates into a 3.5% increase in caseloads.  This result is significant at well more than the 1% level.  Older populations yielded greater COVID caseloads.  This is consistent with the obvious: caseloads (and fatalities) were heavily concentrated on older people.  So, yes: a confounding factor (age) may explain much of what is going on.  But, vaccinations still don’t appear to have reduced caseloads.  NPI’s, meanwhile, still have the appearance of driving caseloads.

Now, let’s consider feedback effects.  A yet more elaborate method of estimation might go some way toward accommodating feedback (if any) between caseloads, vaccinations, and the stringency of NPI’s.  We might pose not a single regression equation but rather a system of equations.  One equation could model caseloads as a function of vaccinations and NPI’s as well as of variables indicating differences between countries.  Some countries, for example, support older populations.  Older populations have proven to be more susceptible to coronavirus infection.  One can contemplate a second equation that models demand for vaccinations as a function of caseloads, and one could then contemplate an equation modeling the supply of vaccinations.  Similarly, one could yet contemplate an “stringency” equation that models the authorities’ effort to increase or relieve the stringency of their NPI regimes.  Higher caseloads might induce NPI regimes of greater stringency.

Thus far I’ve posed a system of four equations.  That is rather elaborate, and it is not obvious that we have data of sufficient depth or breadth to jointly estimate such an elaborate system.  But, we can avail ourselves of methods of estimating a single equation that is embedded in a system of equations.  A great advantage of “single equation” methods is that they allow us to be largely agnostic about the structure of other equations.  But, we do have to have access to a reasonable number of “instrumental variables,” explanatory variables that are not subject to feedback and yet explain something about the variation of vaccinations and the stringency of NPI’s.  Data on country characteristics would be good candidates. Specifically, I use median age, GDP and population by country.  I find that other variables (such as the proportion of a population susceptible to diabetes) do not add much information not already spanned by age, GDP and population.

With this small number of variables in hand, I estimate a slightly more elaborate equation by “two-stage least squares” (2SLS).  The “first stage” amounts to projecting endogenous variables (variables determined within the hypothesized system of equations) on the set of exogenous variables (variables not determined within the system by feedback effects).  In the second stage, we project the variable of ultimate interest (caseloads) on the projections of the endogenous variables and, possibly, on some of the exogenous variables.  Specifically, I pose a second stage equation that looks like:

ln(Cases) = α + β ln(Projected Vaccinations) + γ ln(Projected Stringency) + δ ln(Median Age) + ε

The results of estimating the coefficients in this equation are featured in the third column in the table above.  The statistical significance of Stringency disappears, but vaccinations again appear to have some effect in driving caseloads.  The elasticity of 0.87 on vaccinations is statistically significant at 5% level.  The elasticity with respect to median age is estimated to be 1.21, but it is not statistically significant.  The R-squared is 42%.

I should report that one infirmity of the 2SLS approach is that the first stage regression (not reported) of Stringency on median age, GDP and population is not very robust.  The “instruments” for Stringency appear to be a little weak.  Be that as it may, it may be the case the that feedback really had little to no effect on the stringency index, averaged over 2020-2021.  (A Hausman test yields results suggesting just that: We can treat Stringency, averaged over 2020-2021, as an exogenous factor, but vaccinations are endogenous and may be generating important feedback.)  This motivates the fourth and last estimation method.  I estimate the following equation by 2SLS:

ln(Cases) = α + β ln(Projected Vaccinations) + γ ln(Stringency) + δ ln(Median Age) + ε

The results derived from this fourth estimation look very, very much like the results of the previous estimation with one important exception: the estimated elasticity of 1.49 on Stringency appears statistically significant.

What to make of all of this?  The infirmities of any one estimation method notwithstanding, expert opinion was wrong: we cannot conclude that vaccination regimes and NPI regimes reduced caseloads.  Indeed, at best, NPI’s and vaccinations had no effect on caseloads, but there are strong signals in the data indicating that NPI’s and vaccinations increased caseloads. 

Regression analysis of coronavirus fatalities –

Let’s now turn our attention to counts of fatalities attributed to coronavirus infection.  I apply to coronavirus fatalities the same four estimation methods I applied to caseloads.  I report those results in the following table:

There are both important similarities and differences between these results and the results that pertain to caseloads (reported in the table above).  As above, vaccinations and NPI’s have the appearance in the naïve regression of increasing coronavirus fatalities. Controlling for age (the second regression) knocks out the apparent effect of vaccinations (as above), but the third regression looks different.  It looks like little more than noise.

Hausman tests suggest that feedback from coronavirus fatalities to Stringency and vaccinations is not an important phenomenon.  By that reasoning, the second estimation (by OLS) would be defensible.  Even so, the fourth specification does accommodate feedback, and both it and the second estimation method suggest what?: Age distribution drives much of the action.  NPI regimes also appear to have induced fatalities.  What can we not say?: We cannot argue that NPI’s and vaccinations reduced fatalities.  We can say that the experts were wrong.

Regression analysis of all-cause mortality/excess mortality?

Examining the effects of NPI’s and vaccination campaigns on case counts and COVID fatalities is one thing.  Better it would be to examine the effects of NPI’s and vaccination campaigns on all-cause mortality.  After all, the questions we really care about include: Did NPI’s and vaccination campaigns actually save lives?  Did they mitigate the toll of the entire coronavirus phenomenon?  Did they or did they not induce a non-trivial volume of fatal or debilitating “adverse effects”?  Did NPI’s induce a non-trivial volume of non-COVID fatalities?

We should ask such questions for at least two reasons.  One is that it could very well be the case that the COVID toll did not contribute one-for-one to total mortality.  (It did not.  I hope this is old news.)  Many people who succumbed to COVID may have been likely to succumb to underlying “co-morbidities,” anyway.  We know that the COVID toll was concentrated on people who were very unhealthy to begin with; these people were not likely long for the world.  Harsh, perhaps, but less harsh than the COVID toll being concentrating on young people—people who would yet have decades of high-quality life ahead of them.  Instead, COVID took away people who were already susceptible to succumbing to other conditions.  Accordingly, it is reasonable to wonder what volume of fatalities attributed to COVID would have occurred anyway.  Coronavirus fatalities may not map one-to-one into total mortality.  The second reason is (again) that there is some question of whether NPI’s and vaccination campaign may themselves have induced—and continue to induce—appreciable volumes of non-COVID fatalities. 

I would report results for “excess mortality” from regression analyses that parallel the analyses reported above for caseloads and coronavirus fatalities.  It turns out that the data only support analysis of data derived from 75 countries.  (The principal difficulty is that not all countries provide data sufficient to calculate excess mortality.)  Being limited to 75 countries is not a problem per se.  The problem is that those 75 countries are not representative of the 170 or so countries featured in the other analyses, and those 75 countries are surely not representative of the 228 jurisdictions indicated in the entire dataset.  (Some “jurisdictions” are island possessions of other countries.)  For example, all of the countries of Africa except for South Africa and Egypt disappear from the analysis.

What to do?  I put analysis of all-cause mortality/excess mortality aside, and examine changes in the stringency of NPI’s over time.  The data support aggregation on a monthly basis without losing too many countries.  Weekly data would be preferable, but reporting from any one country can be sufficiently irregular to mess that up.

Regression analysis of the timing of NPI’s –

The evidence suggests that countries tended to ratchet up the stringency of NPI’s as COVID fatalities mounted but just as COVID caseloads were declining.  So, like an unlucky surfer, the authorities tended to miss the wave that would potentially matter (rising caseloads) and implement stricter NPI’s just as the lagged consequences of rising caseloads (rising COVID mortality) imposed itself.

Note the dynamic.  Rates of mortality rise.  The authorities implement stricter NPI’s.  Caseloads are already falling.  Rates of mortality will then naturally fall, but then the authorities declare victory.  They observe that rates of mortality eventually declined some time after the implementation of stricter NPI’s.  But they ignore the fact that rates of mortality were going to decline absent the ratcheting up of NPI’s.  They have no business declaring that NPI’s had any effect on mortality, because the observed pattern is consistent with NPI’s having no effect.

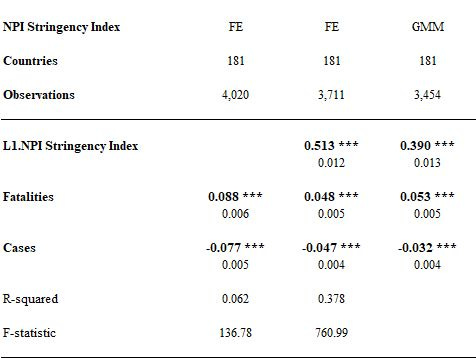
To see this, consider the regression results reported in the following table.  The data support analysis of “panel data”.  Specifically, we can track the progress of 181 countries over the span of two years.  (Not all of the 181 countries provided data over these entire two years.)

I map the Stringency Index (measured month to month) against monthly COVID fatalities and monthly caseloads.  In the last two specifications, I map Stringency on the one-month lag of Stringency itself.  The idea here is that inertia in the stringency of NPI regimes may be an important phenomenon.  I model stringency with a lag as a check on the robustness of the basic conclusion that NPI’s increase with the increase in fatalities but also decline with the decline in caseloads.

The first two analyses feature “fixed effects” (FE) regressions.  Basically, we assign a dummy variable to each country and thereby sweep away country-specific effects.  Doing that allows us to zoom in on an effect (if any), averaged across all countries, of changes in rates of COVID fatality and COVID cases on the implementation of NPI’s.  The last method (GMM) amounts to a two-stage regression analysis according to which we project the lag of stringency on lagged values of fatalities and caseloads.  (I apply the Arrelano-Bond estimator.)  It amounts to another robustness check, although it involves its own set of heavy assumptions.

The reported coefficients are elasticities.

What do we see?  Let me focus on the second regression.  A doubling in fatalities from one month to the next—a 100% increase—corresponds to about a 5% increase in the Stringency Index.  Similarly, a doubling of the case rate from one month to the next corresponds to about a 5% decrease in the Stringency Index.  I am not saying that changes in case rates or rates of mortality cause changes in NPI’s. I could thus have dispensed with the GMM estimation, but the correlations are consistent with the proposition that NPI’s chase after rates of COVID mortality at the same time that case rates are falling.  The experts miss the wave, and it is not obvious that NPI’s reduce case rates or mortality, anyway.  Indeed, the analyses we reviewed earlier suggest that NPI’s fail to contain either case rates or COVID mortality.

As I have already suggested, a complete analysis of the welfare effects of NPI’s—lockdowns, school closures, mask mandates—and “vaccination” campaigns would include the effects of these things on total mortality.  These things may have exacerbated the COVID toll and likely induced mortality and debilitating effects.  These effects may yet pan out over the course of years.  But, that is not the end of the story.  A complete analysis would also include economic effects.  How much did we pay to harm ourselves?  How much economic activity did we give up to harm ourselves?  And what do we do to impose some accountability on the self-anointed, best-and-brightest experts going forward?

---

[1] https://www.cbsnews.com/video/dr-fauci-mask-rules-shouldnt-be-decided-by-a-judge-with-no-experience-in-public-health/

[2] https://www.foxnews.com/media/fauci-wants-courts-defer-public-health-experts-public-health

[3] Rubin, Rita, “COVID-19 Vaccines Have Been Available in the US for More Than a Year—What’s Been Learned and What’s Next?, Journal of the American Medical Association, January11, 2022 posted at https://jamanetwork.com/journals/jama/fullarticle/2788213.